Refraction

To a man standing in water seem his legs to be shorter. The wave theory of light explains this impression by a lower light speed c in a substance relative to that c₀ in vacuum. Quantitative formula for this decrease of speed is given by empirical refractive index n, which is expressed as a ratio of the speed of light in vacuum c₀ relative to that c in the substance: n = c₀/c. For air is the refractive index about n = 1,00029, for water 1,33 and for glass 1,55.

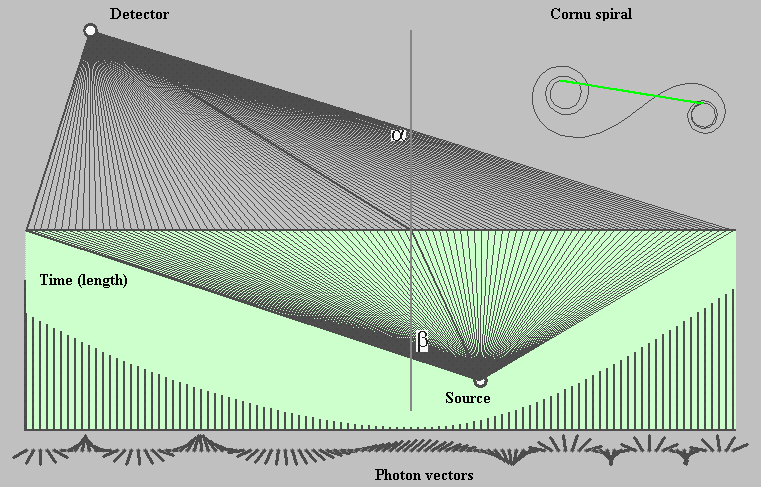
Fig. 13. Refraction (refraction.exe)

In our computer programs we simulate the light phenomena by the sum-over-paths method where photon is the basic particle of the light. By definition, a photon is a particle, which travels at the speed of lightc₀ in vacuum. So the light speed decrease in materials is the result of the zigzag movement of the photon. In the section Point-to-Point paths, the refractive index is expressed as a ratio of the mean length L of the zigzag path between two points relative to the straight-line distance L₀ of the considered points: n =L/L₀.

Fig. 13 illustrates the refraction effect as it is simulated by the program refraction.exe. Source of the light is in water (substance). The paths of photon are shown as straight-line segments. In calculation of the path length from the source to the detector, the lengths of segments in substance is multiplied by the refractive index n. The graph in the bottom of Fig.13 shows time photon needs to reach the detector. Measure for time calculation is the length of the path. Below the graph, photon vectors are depicted in direction as they ended on the detector over relevant paths.

In the vicinity of the shortest time the directions of the photon vectors are nearly the same because the timing of their paths is nearly the same. It is evident that photon vectors in the vicinity of the shortest time make the major contribution to the endpoints distance of the Cornu spiral. It is right to say that the light goes where the time is the least.

The sum-over-paths method reveals the Fermat’s least time principle of classic optic (Fermat Pierre 1601-1665). The least time path is shown in the bold line in Fig. 13. The figure illustrates as well the Snell’s law which relates the refraction index n of the two media to the directions of propagation in terms of the angles to the normal n = c₀/c = sinα /sinβ . It means that a medium with greater refractive index bends the light ray towards the normal to the boundary between the two media.