Principles

Feynman’s strange theory of light constructs its conclusions on following three principles

Principle A

Photon is an elementary particle, the quantum of electromagnetic radiation. It is basic unit of light.

Principle B

We are able calculate only the probability of reaching designated point in space by a photon emanated from a point source.

Principle C

To compute the probability, we must take into account all alternative paths
between point source and the given point in space.

Photon as the quantum of electromagnetic radiation is defined by two attributes of its existence

a) Photon travels at speed of light about c₀ = 3.108 [m/s].

b) Photon’s energy is e = h.ν, where h = 6,6.10-34 [Js] is Planck’s constant and n is frequency of light.

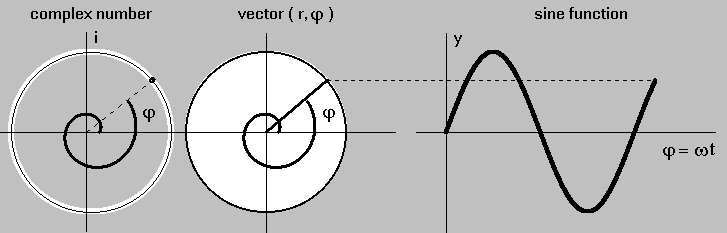
Fig. 1. Three representations of sinusoid (sinusoid.exe), (vector-sum.exe)

Light is an electromagnetic radiation in the visible range of wavelengths; nevertheless, conclusions derived by strange theory of light are valid for any wavelength in the range from the long radio waves to X-rays. When one says frequency, we have in mind a sinusoidal oscillation y = sin φ, which can be shown in three forms (Fig. 1). The vector form, defined by vector length (magnitude) r and its phase angle φ, is applicable in a case where a result of two or more parallel events is calculated. Adding two or more vectors gives the sum vector (resultant vector of summation), which connects the initial point and the terminal point of the vector addition (Fig. 2).

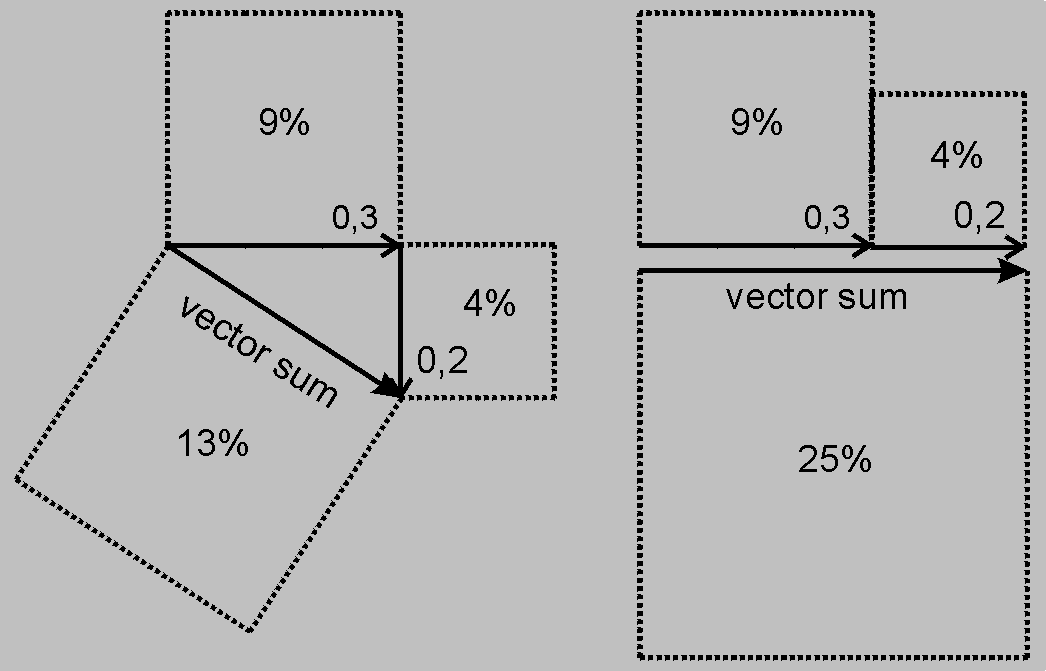
Fig. 2. Probability equals squared length of the sum vector

The points in complex number plane define the sine function by the imaginary part in the Euler’s formula re^iφ = r(cosφ + i sinφ). This form is suitable for serial event calculation when two sine functions are to be multiplied. Multiplication of two or more exponential expressions yields a vector whose length is the product of involved vectors magnitudes and its phase equals to sum of involved vectors phase angles.

Below we indicate the rules on which the calculations in our programs are based. If you ask why they are so strange, the answer is that they are part of the Feynman’s discovery, which yields to matching the calculation of results with experiments.

Rule 1. Photon is visualised by a vector, which rotates at a light frequency during its travel along the path.
Rule 2. The phase angle of the vector in target point is the product of the frequency n and the path length L from point source to target. The length of the path is the measure for time in our calculations.
Rule 3.The sum vector (resultant vector) in the target point comes from the sum of vectors over all alternative paths.
Rule 4. Probability of photon falling into target equals to square of the sum vector length.

One question still remains; how can we take into account all alternative paths? We are going to give an answer to it in the Point-to-Point paths section.

Computation approach to the above given rules is known as “the path integral method”, “the sum over histories method” or “the sum over paths method”, as we prefer to call it in our text. An advantage of this method consists of its illustrative nature and no necessity of using complex mathematics. No differential equations, no operators, etc. are needed. In our animation programs we make do with adding vectors and computing the length of path compiled from straight lines. The sequence of adding vectors is for the sum of vectors irrelevant since summation obeys the commutative low; nevertheless, systematic computation sequence yields nice Cornu spiral visualising the calculation progress.