Point to Point paths
We are going to calculate the probability that a photon, which emerged from a point source, falls onto a detector point. According to the QED method we ought to evaluate all alternative paths, as we do not know which of them the photon travels over. Graphically the photon is represented by a vector, which rotates along the path at a frequency of light (of photon) ν. The final angle of the vector on the detector is the product of path length and frequency ν. This vector is added to the sum of vectors that travel along other paths. The result of adding of all these vectors is the global vector sum.
We are not able to explore all alternative paths. However, in our global-vector-sum.exe program we show that a straight line connecting the point source with the detector point is the one, which can represent all paths. The path is formed of straight-line pieces con-nected to each other in breakpoints (Fig. 3). In the program, their number can be selected and a random number generator determines their positions. The breakpoint positions are restricted to corridors whose width is step-by-step getting narrower and limiting to the straight-line. For a narrow corridor the vector sum of all paths is much longer than that for a broad one.
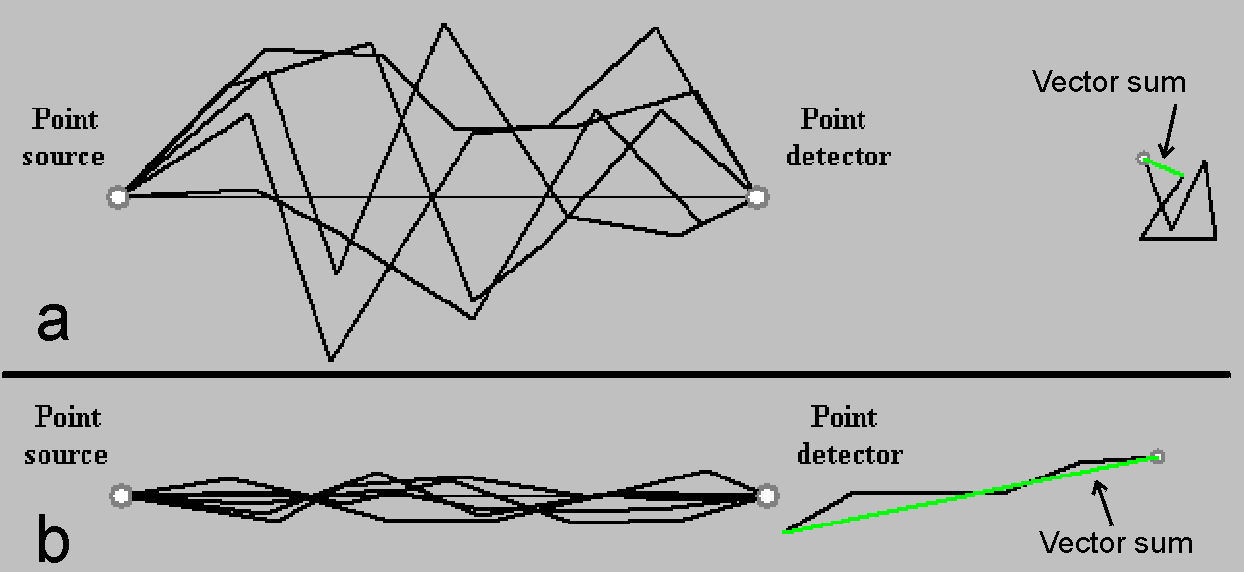
Fig. 3. Corridor paths and they vector sum (corridor-vector-sum.exe)
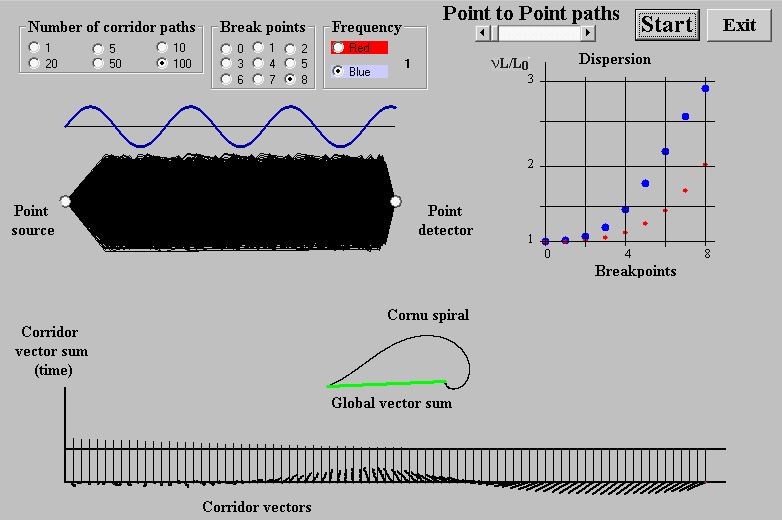
Fig. 4. Point to point paths (global-vector-sum.exe)
Average path lengths of the particular corridors are aligned to graph in the lower part of the Fig. 4. The horizontal straight-line exposes the source to detector distance. The corridor vectors sums are displayed along the horizontal axis of the graph. As the corridor is getting narrower, vectors point practically in the same direction, which means that mainly they contribute to the length of the global sum of vectors of all corridors (Cornu spiral). In other words, all paths closely plaiting to the straight-line path determine the global vector sum and for an observer it seams like that the light spreads as straight-line rays. In all our programs and texts, speaking about vector sum of pats from a point source to a detector point, we have in mind the global vector sum in Fig. 4.
The commutative law holds for vector adding. It means that the vectors can concatenate in any sequence without changing the resulting vector: the vector sum that connects the initial point of the first vector to the end of last one. The graphic image of the vector sequence is irrelevant, it only reveals the adding sequence. If summation order is well arranged, the vector sequence takes a nice spiral labelled Cornu spiral. The global sum vector in Fig. 4 also connects the initial point to the terminal point of Cornu spiral, even thought if it is far away to be like a spiral. We will see nice Cornu spirals in the next sections.
In vacuum there are no obstacles (atoms), which cumber photon in his free travel. The program simulates this idea for zero number of breakpoints. The length of a straight-line path between the source and the detector is L0. For a growing breakpoints number the path length L is getting longer and the global vector sum is getting shorter due to the zigzag path. The L/L0 ratio is a material constant. Its multiple by frequency of the light is labelled as the refractive index n = νL/L0 = νV0/V, where V0 is the length of global vector without breakpoints, and V with them. Schoolbooks refer to refractive index as to a ratio of the speed of light c0 in vacuum relative to that c in the substance n = c0 /c. However, in a substance a photon moves at the speed c0, as defined, but along a zigzag path, which takes more time to reach the detector. This is a simplified view on refractive index related to the Fig.3 and Fig.4. Feynman explains refractive index more comprehensively in his lecture http://feynmanlectures.caltech.edu/I_31.html.
Diagram in the upper right-hand corner in Fig. 4 illustrates the refractive index νL/L0 of blue and red lights. One period of the sinusoid, shown over paths, depicts the wavelength of the selected colour light. The frequency of the blue light is twice higher with respect to red, so its wavelength is two times shorter. The material constant L/L0 is represented by breakpoints at the horizontal axis. The frequency dependence of the refractive index is labelled as dispersion, which manifests itself always when a light crosses the boundary of substances with different refractive indexes. The phenomenon of dispersion makes it felt in several forms, as can be seen in further sections.
Published values are absolute refractive indices na as refractive index of vacuum is assumed 1 per definition. In our notation it takes the form na = νL/L0/νLvc/L0= L/Lvc, where Lvc is the average length of photon path in vacuum. We have derived an important relation L = naLvc, which we use in our programs for simulation of diffraction in specific situations. For the visible light most transparent media have indices between 1 and 2. A few examples are given in the table below. These values are measured at the yellow light with a wavelength of 0.589 micrometer. Germanium is transparent and has the refractive index of about 4 for radiation in range of micrometers, making it an important material for thermo imaging optics.
| Matter | Refractive index na=c0/c | Remark |
| Vacuum | 1 | per definition |
| Air | 1.000293 | yellow light |
| Water | 1.333 | yellow light |
| Glass | 1.6 to 1.9 | yellow light |
| Diamond | 2.42 | yellow light |
| Silicon | 3.96 | yellow light |
| Germanium | 4 | infrared radiation |
Photon travels over a zigzag path even in vacuum; after all, it reaches any point of the space with a certain probability. Because the absolute refractive index is defined relatively to that of vacuum, we assume that the average length of paths in vacuum equals to the straight-line distance from the detector point to the source point: Lvc = L0.