Dispersion

By the word dispersion we usually denote a separation of light to its frequency components. The wave theory explains this separation by a frequency dependence of the material’s refractive index n, which is expressed as a ratio of the speed of light in vacuum c₀ relative to that c in the substance: n = c₀/c.

In our computer program we simulate the dispersion phenomenon on the bases of the sum-over-paths method, where photon is the basic particle of the light, which moves at the speed c₀ of light in vacuum. Therefore, the light speed decrease in materials is the result of a zigzag movement of the photons. In the section Point-to-Point paths, the refractive index is expressed as a ratio of the mean length L of the zigzag path between two points relative to the straight-line distance L₀ of the considered points: n = L/L₀. This equation is used in the program for computing the length L in a matter (glass) with given refractive index n and the straight-line distance L₀ of initial points on an air-glass boundary and the terminal points on screen.

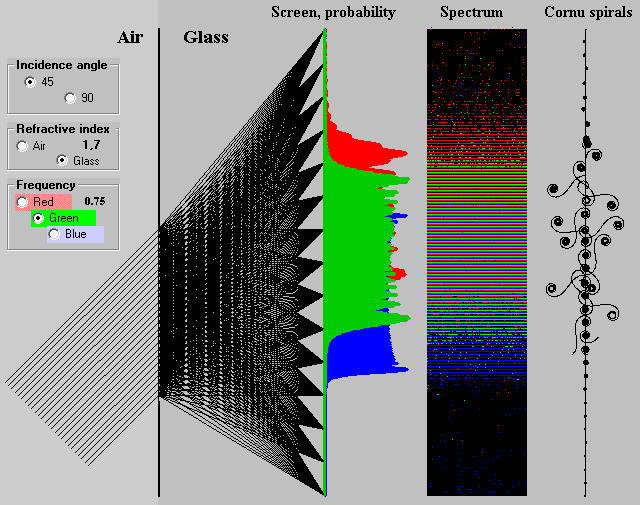
Fig. 15. Dispersion (dispersion.exe)

The Fig. 15 illustrates the dispersion. A mixture of three monochromatic lights (red, green and blue) is accident on the air-glass interface at a not-perpendicular angle. Separation of the R, G, B components is depicted by their interference patterns in corresponding colours. Spectrum illustrates the light, as it would be seen on a screen. On the right-hand side of the Fig. 15 there are shown some Cornu spirals, which have formed the green interference pattern at the relevant points. Interference patterns in Fig.15 confirm the frequency dependence of the refraction effect. Blue light is refracted more than the green and the red ones