Lens

Geometric optics define a focus as a point at which rays meet after refraction in lens when the incoming beam makes a zero angle with the axis of the lens. From the viewpoint of the sum-over-paths method, a focus is a point in which the probability of hitting the lens axis by photon reaches the maximal value when photon incident paths are parallel to the lens axis (Fig. 16).

To compute the length of the photon path, the slower speed of light in lens is taken into account by multiplying the path segment in the lens by the refractive index n of the lens substance. At the focus all paths should have the same length to be achieved that all photon vectors point to the same direction and the vector sum to acquire the maximal value (we remind that square of the vector sum is the measure for probability). Parabolic shape of lens fulfils these conditions. Spherical form is a good approach to an ideal shape, but it is not the best one as it appears in the camber form of Cornu spiral in focus (Fig. 16).

The above-mentioned insufficiency of spherical lens can be made less by an aperture taking smaller (lens.exe), which excludes the boundary parts of the lens and the shape of the lens is approaching the ideal parabolic form. The improvement appears on the Cornu spiral, which is now practically a straight line. At the same time, the focal length is enlarged and the probability pattern is getting wider (the lens gives a deep sharp image in the camera).

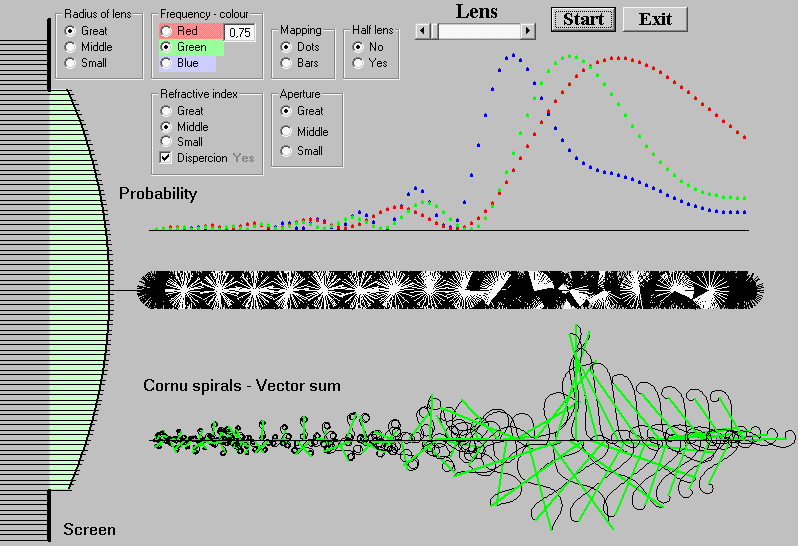
Fig. 16. Focus is point at which probability reaches maximum (lens.exe)

A dispersion at the boundary of air and water/glass manifests itself by a separation of colours in incident light, as we discuss it in the section Dispersion. In the case of lens, dispersion separates the focuses in such a way that the focus of higher frequency light (blue) is closer to the lens then that of the lower frequency light (green, red). Shifting the focuses, labelled as aberration of an optical system, appears as coloured boundaries in colour photographs.

With the program lens.exe we can simulate a situation which cannot be observed in nature. We can compute the probability pattern without existence of the dispersion. In this case no separation of the focuses takes place even by spherical lens. Only width of the probability pattern is influenced by the frequency of the light.